Κεφάλαιο 9: Πλάκες και δίσκοι
|
1. Πλάκες
1.1. Πεδίο εφαρμογής
Το άρθρο αυτό ισχύει για συμπαγείς πλάκες υποβαλλόμενες σε κάμψη ενδεχομένως δε και σε ορθές αξονικές δυνάμεις που δρουν παράλληλα προς το μέσο επίπεδο της πλάκας. Ισχύει επίσης για πλάκες με μη ομοιόμορφο πάχος (π.χ. πλάκες με νευρώσεις, πλάκες με σώματα πλήρωσης, πλάκες μεταβλητού πάχους κ.α.) υπό την προϋπόθεση ότι η συμπεριφορά τους έναντι των φορτίσεων μπορεί με ικανοποιητική προσέγγιση να εξομοιωθεί με την συμπεριφορά ισοδύναμης πλάκας συμπαγούς διατομής.
1.2. Μέθοδοι ανάλυσης
Τα εντατικά μεγέθη μπορούν να καθορισθούν με μεθόδους που έχουν ως βάση:
α) την ελαστική ανάλυση και
β) την πλαστική ανάλυση, η οποία μπορεί να χρησιμοποιείται μόνο για μετέλεγχο υφιστάμενης κατασκευής.
1.3. Ελαστική ανάλυση
Η μέθοδος αυτή βασίζεται στην θεωρία ελαστικότητας κατά την οποία υποτίθεται γραμμική σχέση μεταξύ τάσεων και παραμορφώσεων (νόμος Hooke).
1.3.1. Γραμμική ανάλυση
Η γραμμική ανάλυση μπορεί να γίνει με βάση τις ονομαστικές διατομές και με τιμή του λόγου του Poisson μεταξύ 0.00 και 0.20.
Τα αποτελέσματα της γραμμικής ανάλυσης μπορούν να χρησιμοποιηθούν για τους ελέγχους και έναντι οριακών καταστάσεων αστοχίας και έναντι των οριακών καταστάσεων λειτουργικότητας.
1.3.2. Γραμμική ανάλυση με περιορισμένη ανακατανομή
Η γραμμική ανάλυση με περιορισμένη ανακατανομή μπορεί να εφαρμοσθεί για τις ίδιες συνθήκες πλαστιμότητας και ανακατανομής όπως και στους γραμμικούς φορείς.
Στις συνεχείς πλάκες με γραμμικές στηρίξεις, οι ροπές στήριξης που προκύπτουν από γραμμική ανάλυση μπορούν να μειωθούν ή να αυξηθούν μέχρι 15%, χωρίς έλεγχο, με την προϋπόθεση ότι θα διορθωθούν και οι αντίστοιχες ροπές των ανοιγμάτων, ώστε να ικανοποιούνται οι συνθήκες ισορροπίας.
1.4. Πλαστική ανάλυση
Γενικώς η πλαστική ανάλυση (παράγραφος 9.1.2) εφαρμόζεται για τις οριακές καταστάσεις αστοχίας έναντι εξωτερικών φορτίων (άμεσων δράσεων) και μπορεί να γίνει με βάση τις στατικές ή κινηματικές μεθόδους. Για να επιτρέπεται η εφαρμογή της μεθόδου πρέπει να ικανοποιούνται οι παρακάτω συνθήκες:
1) Ο εφελκυόμενος οπλισμός σε κάθε σημείο και προς κάθε κατεύθυνση δεν πρέπει να υπερβαίνει το μισό εκείνου που αντιστοιχεί σε διατομή για την οποία η οριακή κατάσταση αστοχίας σε κάμψη χαρακτηρίζεται από τις παρακάτω παραμορφώσεις (Σχήμα 10.1):
εs = εyd και εc = -0.0035 (9.1)
2)α) Εάν εφαρμόζεται στατική μέθοδος, πρέπει η κατανομή ροπών που εκλέγεται να μην διαφέρει σημαντικά από μία ελαστική κατανομή ροπών, ο λόγος των χρησιμοποιούμενων ροπών στήριξης προς τις τιμές τους, οι οποίες θα προέκυπταν από μία ελαστική ανάλυση πρέπει να κείται μεταξύ:
0.50 και 1.25 για χάλυβες θερμής έλασης,
0.75 και 1.25 για χάλυβες ψυχρής κατεργασίας,
0.85 και 1.15 για δομικά πλέγματα και τένοντες με συνάφεια.
2)β) Εάν εφαρμόζεται κινηματική μέθοδος, πρέπει ο λόγος των ροπών στήριξης προς τις ροπές ανοίγματος να κείται μεταξύ:
0.50 και 2.00 για χάλυβες θερμής έλασης,
0.75 και 1.33 για χάλυβες ψυχρής κατεργασίας,
0.85 και 1.15 για δομικά πλέγματα και τένοντες με συνάφεια.
1.5. Γενικές διατάξεις για την ανάλυση πλακών που στηρίζονται σε δοκούς ή φέροντες τοίχους
Η ανάλυση πλακών που στηρίζονται συνεχώς κατά μήκος της περιμέτρου των σε δοκούς ή φέροντες τοίχους (από τοιχοποιία), μπορεί να βασισθεί στην παραδοχή ελεύθερα στρεπτών αλλά ανυποχώρητων στηριγμάτων. Πλάκες που στηρίζονται σε σιδηροδοκούς ή προκατασκευασμένες δοκούς από οπλισμένο σκυρόδεμα θεωρούνται ως συνεχείς μόνον αν η επάνω επιφάνεια της πλάκας βρίσκεται τουλάχιστον 40 mm πάνω από το επάνω πέλμα των δοκών και ο οπλισμός της πλάκας συνεχίζεται πάνω από τη δοκό στο επόμενο άνοιγμα (προς κάλυψη των ροπών στήριξης).
Στις στηρίξεις συνεχών πλακών η ροπή υπολογισμού αναφέρεται στον άξονα της στήριξης για έδραση σε φέροντα τοίχο ή στις παρειές της στήριξης για μονολιθική σύνδεση με το στήριγμα.
Για τον υπολογισμό των εντατικών μεγεθών πλακών, οποιασδήποτε μορφής και είδους στήριξης, ισχύουν γενικά οι βάσεις υπολογισμού των εντατικών μεγεθών.
Προσεγγιστικές μέθοδοι επιτρέπονται όταν βρίσκονται προς την πλευρά της ασφαλείας.
Για ορθογωνικές τετραέρειστες πλάκες επιτρέπεται να εκτελείται υπολογισμός κατά προσέγγιση, με την παραδοχή διασταυρούμενων λωρίδων πλάκας με κοινό μέγιστο βέλος κάμψης. Οι υπολογιζόμενες ροπές ανοίγματος σύμφωνα με τις παραπάνω παραδοχές, πρέπει να αυξάνονται κατάλληλα όταν:
α) οι γωνίες δεν εξασφαλίζονται έναντι ανύψωσης,
β) δεν διατάσσεται οπλισμός συστροφής σε γωνίες όπου συναντώνται δύο πλευρές στήριξης ελεύθερα στρεπτές,
γ) υπάρχουν οπές στις γωνίες, οι οποίες επηρεάζουν σημαντικά τη δυστρεψία.
Συνεχείς τετραέρειστες πλάκες με λόγο θεωρητικών ανοιγμάτων min l / max l κατά μια διεύθυνση συνέχειας όχι μικρότερο από 0.75 επιτρέπεται για τον υπολογισμό των ροπών στήριξης να θεωρούνται ως πλήρως πακτωμένες στις στηρίξεις. Οι μέγιστες και οι ελάχιστες ροπές ανοίγματος επιτρέπεται να υπολογίζονται με τη θεώρηση πλήρους πάκτωσης για την καθολική φόρτιση p (όλων των ανοιγμάτων).
p = 1.35 g + 1.50 q/2 (9.2)
και ελεύθερα στρεπτής έδρασης στις στηρίξεις για φόρτιση p με διάταξη ζατρικίου
p = 1.50 g ± 1.50 q/2 (9.3)
όπου g, q το μόνιμο και το κινητό φορτίο της πλάκας, αντίστοιχα.
Οι αντιδράσεις τετραέρειστων ομοιόμορφα φορτισμένων πλακών, οι οποίες χρησιμοποιούνται για τον υπολογισμό των δράσεων του σχεδιασμού των δοκών, επιτρέπεται να υπολογίζονται από τις επιφάνειες φόρτισης που προκύπτουν από γεωμετρικό μερισμό της επιφάνειας της κάτοψης.
Στηρίξεις που δεν ελήφθησαν υπόψη στον υπολογισμό της πλάκας πρέπει να συμμετέχουν στη διανομή των φορτίων της πλάκας.
1.6.1. Διανομή σημειακών, γραμμικών ή τμηματικώς κατανεμημένων φορτίων σε αμφιέρειστες πλάκες
Εφόσον δεν γίνεται ακριβέστερη ανάλυση, επιτρέπεται για φορτία σημειακά, γραμμικά ή ομοιόμορφα κατανεμημένα σε ορθογωνική επιφάνεια της πλάκας, να καθορίζεται υπολογιστικό πλάτος διανομής του φορτίου bm, εγκαρσίως προς την διεύθυνση του κυρίου οπλισμού. Το πλάτος t της εισαγωγής του φορτίου (στο μέσο επίπεδο της πλάκας) ισούται με την αντίστοιχη διάσταση της επιφάνειας εφαρμογής του φορτίου αυξημένη κατά το διπλάσιο του πάχους της επικάλυψης της πλάκας (s) και κατά το πάχος της πλάκας.
Μετά την αναγωγή του σε ορθογωνική επιφάνεια tx x ty στο μέσο επίπεδο της πλάκας, το φορτίο μπορεί να θεωρηθεί ότι αναλαμβάνεται κατά την κύρια διεύθυνση οπλισμού από λωρίδα πλάτους bm. Μέσα στην λωρίδα αυτή θεωρείται ότι δρα σταθερή ροπή κάμψης m ανά μέτρο πλάτους, καθώς και σταθερή τέμνουσα δύναμη ν ανά μέτρο πλάτους.
Τα μεγέθη m και v υπολογίζονται από τους τύπους:
m = Μ / bm (9.4)
v = V / bm (9.5)
όπου:
m ροπή ανοίγματος, mf, ή ροπή στήριξης, ms, (ανά μέτρο πλάτους),
v τέμνουσα δύναμη στη στήριξη (ανά μέτρο πλάτους)
Μ μέγιστη ροπή της πλάκας (ανάλογα με το στατικό σύστημα, από τον Πίνακα Σ9.1.), η οποία φορτίζεται από το συνολικό φορτίο ομοιόμορφα κατανεμημένο επί μήκος tx,
V τέμνουσα δύναμη της πλάκας στην στήριξη.
Ο πρόσθετος οπλισμός που προκύπτει από τα παραπάνω εντατικά μεγέθη τοποθετείται στην πλάκα σύμφωνα με την παράγραφο 18.1.5.1.
1.7. Ανάλυση πλακών χωρίς δοκούς
Η ανάλυση πλακών που στηρίζονται απευθείας και μονολιθικά σε υποστυλώματα, με περίπου ορθογωνική διάταξη σε κάτοψη, μπορεί να γίνει με την μέθοδο των ισοδύναμων πλαισίων. Η μέθοδος αυτή εφαρμόζεται κυρίως για κατακόρυφα φορτία.
Στην περίπτωση κατά την οποίαν η μέθοδος εφαρμόζεται και για οριζόντια φορτία, θα λαμβάνεται το πλάτος συνεργασίας της δοκού l'x από την σχέση
l'x = bo + 2 x hs
όπου:
bo το πλάτος υποστυλώματος στην εξεταζόμενη διεύθυνση και hs πάχος της πλάκας.
Σε αυτήν την περίπτωση δεν χρειάζεται κατά την ανάλυση του φορέα περαιτέρω μείωση της δυσκαμψίας λόγω ρηγμάτωσης (βλέπε παράγραφο 8.2.1).
1.7.1. Κατά πλάτος κατανομή των ροπών ανοίγματος και στήριξης της πλάκας
Για την κατανομή των εντατικών μεγεθών, κάθε φάτνωμα της πλάκας θα πρέπει να χωρίζεται (κατά τις δύο διευθύνσεις) σε μία εσωτερική λωρίδα πλάτους 0.6 l, την λωρίδα ανοίγματος και σε δύο εξωτερικές λωρίδες, λωρίδες στήριξης, εκάστη πλάτους 0.2 l (Σχήμα 9.1).
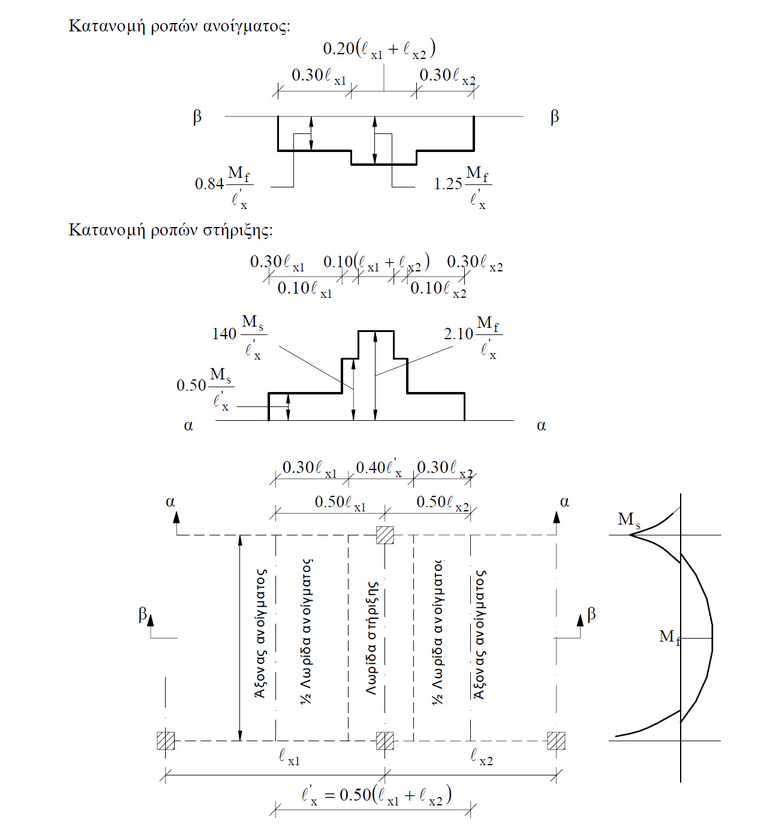
Σχήμα 9.1: Κατά πλάτος κατανομή των μέσων ροπών κατά y
2. Δίσκοι
Οι δυνάμεις που ενεργούν στο μέσο επίπεδο ενός δίσκου μπορούν να προσδιοριστούν με βάση:
| • | ελαστική ανάλυση |
| • | πλαστική ανάλυση |
| • | μέθοδο θλιπτήρων - ελκυστήρων. |
2.2. Ελαστική ανάλυση
Η ελαστική ανάλυση βασίζεται σε γραμμική σχέση τάσεων - παραμορφώσεων (νόμος Hooke). Ελαστική ανάλυση μπορεί να γίνει με βάση τις ονομαστικές διατομές και με τιμή του λόγου του Poisson μεταξύ 0.00 και 0.20.
Τα αποτελέσματα ελαστικής ανάλυσης μπορούν να χρησιμοποιηθούν για ελέγχους και έναντι οριακών καταστάσεων λειτουργικότητας και έναντι οριακών καταστάσεων αστοχίας.
2.3. Πλαστική ανάλυση
Η πλαστική ανάλυση μπορεί να βασισθεί μόνον σε στατικές μεθόδους.
Η πλαστική ανάλυση μπορεί καταρχήν να χρησιμοποιηθεί μόνο για έλεγχο οριακών καταστάσεων αστοχίας.
Παρόλα αυτά, μπορεί να χρησιμοποιηθεί και για έλεγχο οριακών καταστάσεων λειτουργικότητας, εάν οι διαφορές μεταξύ της κατανομής της έντασης που προκύπτει από την πλαστική ανάλυση και της κατανομής της έντασης που προκύπτει από γραμμική ανάλυση είναι αποδεκτές για την υπόψη οριακή κατάσταση λειτουργικότητας.