Συνδεθείτε στην Υπηρεσία Νομοσκόπιο Είσοδος στην υπηρεσία Νομοσκόπιο.     Χρήστης Κωδικός   Υπενθύμιση στοιχείων λογαριασμού       Νέοι χρήστες Εάν είστε νέος χρήστης, θα πρέπει να δημιουργήσετε ένα ΔΩΡΕΑΝ λογαριασμό προκειμένου να φύγει το παράθυρο αυτό και να αποκτήσετε πλήρη πρόσβαση στην υπηρεσία Νομοσκόπιο. Δημιουργία νέου λογαριασμού

1. Γενικά

 

Ο σχεδιασμός των υδραυλικών κατασκευών απαιτεί τη χρήση των εξισώσεων συνέχειας, ενέργειας και ορμής. Από αυτές τις θεμελιώδεις εξισώσεις παράγονται άλλες εξισώσεις με το συνδυασμό των μαθηματικών, των εργαστηριακών πειραμάτων και των μελετών πεδίου. Αυτές οι εξισώσεις χρησιμοποιούνται διαφοροτρόπως για την ανάλυση της ροής σε ανοιχτούς αγωγούς και κλειστούς αγωγούς με 100% πληρότητα. Ένας κλειστός αγωγός με μερική πλήρωση συνιστά ροή ανοιχτού αγωγού. Σε σύγκριση με τους κλειστούς αγωγούς με 100% πληρότητα, η ροή σε ανοιχτούς αγωγούς έχει την πολυπλοκότητα της ελεύθερης επιφάνειας όπου η πίεση είναι η ατμοσφαιρική και αυτή η ελεύθερη επιφάνεια ελέγχεται μόνο από τους νόμους της μηχανικής των υγρών. Μια άλλη πολυπλοκότητα της ροής ανοιχτών αγωγών προκύπτει όταν η κοίτη του ρέματος ή του αγωγού συντίθεται από φυσικά υλικά όπως άμμος, χαλίκια, κροκάλες ή βράχους που είναι μετακινούμενα.

 

Οι μορφές της ροής μπορεί να ταξινομηθούν ως εξής:

 

α. ομοιόμορφη ή ανομοιόμορφη

β. μόνιμη ή μη μόνιμη

γ. στρωτή ή τυρβώδης

δ. υποκρίσιμη (ήρεμη) ή υπερκρίσιμη (ταχεία)

 

Στην ομοιόμορφη ροή, η παροχή και η ταχύτητα παραμένουν σταθερές κατά μήκος της ροής. Στη μόνιμη ροή δε συμβαίνει αλλαγή στη διάρκεια του χρόνου σε μια δεδομένη θέση. Στη στρωτή ροή, το πεδίο ροής χαρακτηρίζεται από επάλληλες στρώσεις του υγρού, οι οποίες δεν αναμειγνύονται μεταξύ τους. Η τυρβώδης ροή χαρακτηρίζεται από την τυχαία κίνηση του υγρού. Η στρωτή ροή διακρίνεται από την τυρβώδη με τη χρήση ενός αδιάστατου αριθμού που ονομάζεται Αριθμός Reynolds. Η υποκρίσιμη ροή διακρίνεται από την υπερκρίσιμη με τη χρήση ενός αδιάστατου αριθμού που ονομάζεται Αριθμός Froude FR. Εάν FR<1 τότε η ροή είναι υποκρίσιμη, εάν FR>1 τότε η ροή είναι υπερκρίσιμη και εάν FR = 1 τότε η ροή καλείται κρίσιμη.

 

2. Ορισμοί

 

Οι ορισμοί που χρησιμοποιούνται στα επόμενα και η έννοια τους πρέπει να ορισθεί είναι:

 

 

3. Βασικές Αρχές

 

3.1. Εισαγωγή

 

Οι βασικές εξισώσεις της ροής αφορούν τη συνέχεια, την ενέργεια και την ορμή (Momentum). Αυτές προκύπτουν από τους νόμους: (1) της διατήρησης της μάζας, (2) της διατήρηση της ενέργειας και (3) της διατήρησης της γραμμικής ορμής, αντιστοίχως. Η διατήρηση της μάζας είναι ένας άλλος τρόπος με τον οποίο δηλώνεται ότι (εκτός από την περίπτωση ανταλλαγής μάζας - ενέργειας) η ύλη ούτε δημιουργείται ούτε καταστρέφεται. Η αρχή της διατήρησης της ενέργειας βασίζεται στον πρώτο νόμο της θερμοδυναμικής ο οποίος δηλώνει ότι η ενέργεια πρέπει να διατηρείται σε κάθε περίπτωση. Η αρχή της διατήρησης της γραμμικής ορμής βασίζεται στο δεύτερο νόμο του Newton της κίνησης ο οποίος δηλώνει ότι η μάζα (του υγρού) επιταχύνεται κατά την κατεύθυνση και κατ' αναλογία των δυνάμεων που επιδρούν πάνω σ' αυτή.

 

Η ανάλυση των προβλημάτων της ροής απλοποιείται πολύ όταν δεν υπάρχει επιτάχυνση της ροής ή αν η επιτάχυνση είναι κυρίως κατά μια κατεύθυνση (μονοδιάστατη ροή), οι επιταχύνσεις ως προς άλλες κατευθύνσεις θεωρείται ότι είναι αμελητέες. Εντούτοις μια πολύ ανακριβής ανάλυση μπορεί να συμβεί όταν κάποιος προϋποθέτει επιταχύνσεις μικρές ή μηδενικές ενώ στην πραγματικότητα αυτές δεν υπάρχουν. Για τις υδραυλικές μελέτες που αφορούν τα οδικά έργα τίθεται ως παραδοχή ότι, η ροή είναι μονοδιάστατη.

 

3.2. Εξίσωση του νόμου της συνέχειας

 

Η εξίσωση της συνέχειας βασίζεται στο νόμο της διατήρησης της μάζας. Για μόνιμη ροή ασυμπίεστων υγρών αυτή είναι:

 

(3.3.2-1)

 

όπου:

V (m/s): η μέση ταχύτητα στην κατακόρυφη διατομή με επιφάνεια Α,

A (m2): η επιφάνεια κάθετη προς τη διεύθυνση της ταχύτητας διατομής της ροής,

Q (m3/s): ο όγκος ροής ή αλλιώς παροχή.

 

Η εξίσωση (3.3.2-1) είναι εφαρμόσιμη όταν η ένταση της ροής είναι σταθερή, η ροή είναι μόνιμη, δεν υπάρχει ουσιαστική πλευρική εισροή ή απώλεια (ή αυτές δε λαμβάνονται υπόψη) και η διεύθυνση της ταχύτητας είναι κάθετη προς την επιφάνεια (βλέπε Σχήμα 3.3.2-1).

 

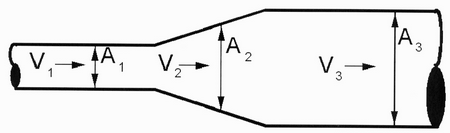
Σχήμα 3.3.2-1: Σχηματική αναπαράσταση του νόμου της συνέχειας

 

3.3. Εξίσωση ενέργειας

 

Η εξίσωση της ενέργειας βασίζεται στον πρώτο νόμο της θερμοδυναμικής ο οποίος δηλώνει ότι η ενέργεια πρέπει να διατηρείται σε κάθε περίπτωση. Για μόνιμη ροή ασυμπίεστου υγρού είναι:

 

(3.3.3-1)

 

όπου:

 

α (-): ο συντελεστής διόρθωσης κινητικής ενέργειας,

V (m/s): η μέση ταχύτητα στη διατομή,

g (m/s2): η επιτάχυνση της βαρύτητας,

p (N/m2): η πίεση,

γ (N/m3): το ειδικό βάρος νερού,

Z (m): το απόλυτο υψόμετρο του κατώτερου σημείου της κοίτης,

hL (m): η απώλεια ενεργειακού ύψους λόγω τριβής και σχήματος,

A (m2): η επιφάνεια της διατομής

 

Ο συντελεστής διόρθωσης κινητικής ενέργειας α είναι για να διορθώνεται η κατανομή της ταχύτητας στην έκταση της ροής. Αυτός επιτρέπει τη χρήση της μέσης ταχύτητας V μάλλον παρά τη σημειακή ταχύτητα v. Ο συντελεστής υπολογίζεται από την εξίσωση:

 

(3.3.3-2)

 

όπου:

 

V (m/s): η ταχύτητα στο σημείο ή η μέση ταχύτητα στο κατακόρυφο επίπεδο

A (m2): η επιφάνεια της διατομής

 

Σημειώνεται ότι ακόμη και σε μια πολύ ανομοιόμορφη κατανομή ταχυτήτων στην έκταση μιας διατομής η διόρθωση είναι μόνο 10%. Συνεπώς ο συντελεστής διόρθωσης της κινητικής ενέργειας κανονικά έχει τιμή ίση με 1,00.

 

Η γραμμή ενέργειας (EGL, energy grade line) αναπαριστά τη συνολική ενέργεια σε μια δεδομένη διατομή οριζόμενη ως το άθροισμα των τριών συνιστωσών της ενέργειας που αντιπροσωπεύεται σε κάθε πλευρά της εξίσωσης (3.3.3-1). Αυτές οι συνιστώσες της ενέργειας συχνά αναφέρονται ως ύψος της γραμμής ενέργειας (velocity head), ύψος πίεσης (pressure head) και ύψος στάθμης (elevation head). Η γραμμή της υδραυλικής κλίσης (HGL, hydraulic grade line) είναι κάτω από την EGL κατά το ποσόν του ύψους της γραμμής ενέργειας, ή αυτή είναι το άθροισμα του ύψους της πίεσης και του υψομέτρου. Η εφαρμογή της εξίσωσης ενέργειας σε ανοιχτούς αγωγούς και σε ροή υπό πίεση αναπαριστάνεται στα Σχήματα 3.3.3-2 και 3.3.3-3 αντιστοίχως.

 

Η εξίσωση της ενέργειας χρησιμοποιείται για τον υπολογισμό της αλλαγής της στάθμης της επιφάνειας του νερού μεταξύ δυο σχετικώς όμοιων διατομών. Μια απλοποιημένη μορφή της εξίσωσης είναι:

 

(3.3.3-3)

 

όπου:

 

V (m/s): η μέση ταχύτητα στη διατομή,

g (m/s2): η επιτάχυνση της βαρύτητας,

d (m): το βάθος νερού στη διατομή,

Z (m): το ελάχιστο απόλυτο υψόμετρο της κοίτης στη διατομή,

hL (m): η απώλεια ενεργειακού ύψους λόγω τριβής και σχήματος μεταξύ των δυο διατομών.

 

Ο δείκτης 1 σε κάθε μεταβλητή της εξίσωσης υποδεικνύει ότι αυτή αφορά στη διατομή στα ανάντη της ροής και αντιστοίχως ο δείκτης 2 ότι αυτή αφορά στη διατομή στα κατάντη της ροής.

 

Η απλοποιημένη εξίσωση είναι εφαρμόσιμη όταν οι υδραυλικές συνθήκες μεταξύ των δυο διατομών είναι σχετικά όμοιες (βαθμιαία μεταβολή ροής) και η κλίση της τάφρου είναι μικρή (μικρότερη από 18%).

 

Η απώλεια του ενεργειακού φορτίου μεταξύ των δυο διατομών συμβαίνει λόγω της τραχύτητας των τοιχωμάτων της τάφρου και άλλους παράγοντες. Αυτές οι τραχύτητες μπορεί να αντιπροσωπεύονται από το συντελεστή τραχύτητας του Manning n και τότε οι ενεργειακές απώλειες μπορεί να υπολογίζονται χρησιμοποιώντας την εξίσωση του Manning:

 

(3.3.3-4)

όπου:

 

L (m): η απόσταση μεταξύ των διατομών,

Q (m3/s): η παροχή,

n (s/m1/3): ο συντελεστής τραχύτητας Manning,

Α (m2): η επιφάνεια διατομής,

R (m): η υδραυλική ακτίνα.

 

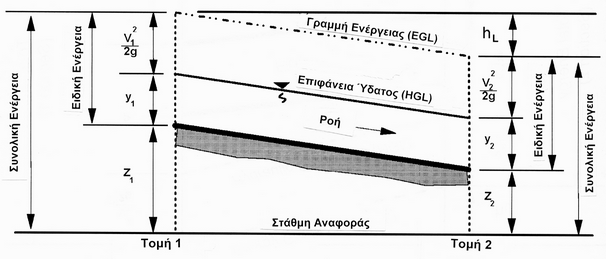
Σχήμα 3.3.3-2: Σκαρίφημα της εξίσωσης της ενέργειας

 

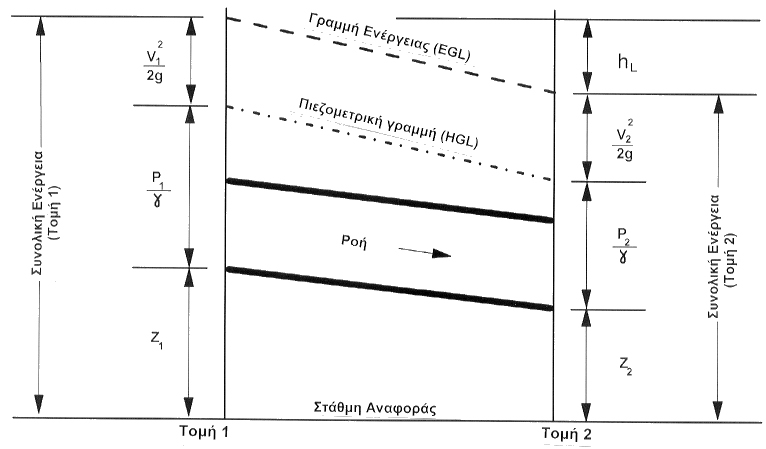
Σχήμα 3.3.3-3:Σκαρίφημα της εξίσωσης της ροής υπό πίεση

 

3.4. Εξίσωση της ορμής

 

Η εξίσωση της ορμής προκύπτει από το δεύτερο νόμο του Newton της κίνησης ο οποίος δηλώνει ότι το αλγεβρικό άθροισμα όλων των εξωτερικών δυνάμεων επί ενός συστήματος ισούται με τη μεταβολή της ορμής. Στην κατεύθυνση x μιας μόνιμης ροής με σταθερή πυκνότητα είναι:

 

(3.3.4-1)

όπου:

 

FX (N): οι δυνάμεις κατά την κατεύθυνση x,

ρ (1000 kg/m3): η ένταση,

β (-): ο συντελεστής ορμής,

Q (m3/s): ο όγκος ροής ή αλλιώς παροχή,

V (m/s): η ταχύτητα κατά την κατεύθυνση x.

 

Ο συντελεστής ορμής διορθώνει την κατανομή της ταχύτητας στην έκταση μιας διατομής της ροής. Αυτός επιτρέπει τη χρήση της ταχύτητας V παρά τη σημειακή ταχύτητα v. Αυτός υπολογίζεται από την εξίσωση:

 

(3.3.4-2)

 

Ο συντελεστής ορμής συνήθως υποτίθεται ότι έχει τιμή ίση με 1,00 επειδή η κατανομή, στην έκταση μιας διατομής, μιας πολύ ανομοιόμορφης ταχύτητας θα πρέπει να απαιτεί μια διόρθωση μικρότερη από 10%. Η εξίσωση της ορμής είναι μια ανυσματική εξίσωση και παρόμοιες εξισώσεις χρησιμοποιούνται για τις άλλες δύο κατευθύνσεις y και z.

 

3.5. Υδροστατική

 

Όταν οι δυνάμεις που επενεργούν επί του υγρού, είναι η πίεση και το βάρος του υγρού η διαφορική εξίσωση της κίνησης σε μια τυχαία κατεύθυνση x είναι:

 

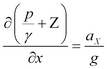(3.3.5-1)

 

Σε μόνιμη ομοιόμορφη ροή (και για μηδενική ροή), η επιτάχυνση είναι μηδενική και η εξίσωση γίνεται:

 

(3.3.5-2)

 

Εντούτοις, όταν υπάρχει επιτάχυνση ο όρος του πιεζομετρικού ύψους p/γ+Z μεταβάλλεται στο πεδίο της ροής. Δηλαδή το πιεζομετρικό ύψος δεν είναι σταθερό στη ροή (βλέπε Σχήμα 3.3.5-1). Στο σχήμα 3.3.5-1(α) η πίεση στον πυθμένα είναι υδροστατική και ισούται με γ x y0, ενώ στην καμπυλοειδή ροή (βλέπε Σχήμα 3.3.5-1 (β) η πίεση είναι μεγαλύτερη από γ x y0 από την προκύπτουσα επιτάχυνση λόγω της αλλαγής της κατεύθυνσης της ροής.

 

 

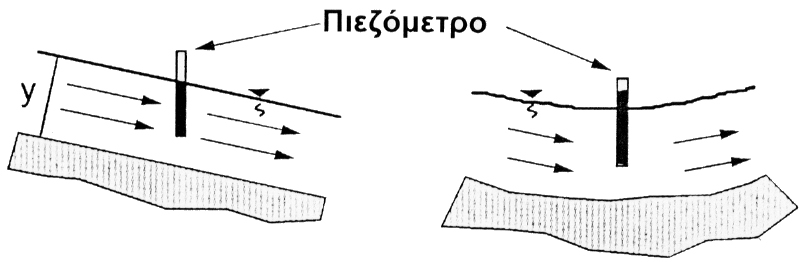
(α - αριστερά) Μόνιμη ομοιόμορφη ροή με κατανεμημένη υδροστατική πίεση

(β - δεξιά) Μόνιμη ανομοιόμορφη ροή με μη κατανεμημένη υδροστατική πίεση

Σχήμα 3.3.5-1: Κατανομή πίεσης σε μόνιμη ροή ομοιόμορφη και ανομοιόμορφη

 

Γενικώς, όταν η επιτάχυνση του υγρού είναι μικρή (όπως στη βαθμιαίως μεταβαλλόμενη ροή) η κατανομή της πίεσης θεωρείται ως υδροστατική. Εντούτοις, για ταχέως μεταβαλλόμενη ροή όπου οι γραμμές του ρεύματος ροής συγκλίνουν, αποκλίνουν ή έχουν ουσιαστική καμπύλωση (καμπυλοειδής ροή), οι επιταχύνσεις του υγρού δεν είναι μικρές και η κατανομή της πίεσης δεν είναι υδροστατική.

 

Στην εξίσωση (3.3.4-5) η σταθερή είναι ίση με μηδέν για μετρούμενη πίεση στην ελεύθερη επιφάνεια ενός υγρού, και για ροή με υδροστατική πίεση σε όλο το υγρό (μόνιμη, ομοιόμορφη ροή ή βαθμιαίως μεταβαλλόμενη ροή) συνεπάγεται ότι το ύψος πίεσης p/γ είναι ίσο με την κατακόρυφη απόσταση κάτω από την ελεύθερη επιφάνεια. Σε κανάλια με κλίση και μόνιμη ροή, το ύψος πίεσης p/γ σε βάθος y κάτω από την επιφάνεια (βλέπε Σχήμα 3.3.5-2) είναι:

 

p/γ = y cos(θ) (3.3.4-6)

 

όπου:

 

y (m): το βάθος μέχρι το εξεταζόμενο σημείο (κάθετη απόσταση μεταξύ πυθμένα και επιφάνειας)

θ (rad): η γωνία μεταξύ του πυθμένα και του οριζόντιου επιπέδου, που συνήθως είναι μικρή και επομένως cos(θ)~1 για κλίσεις <10%

 

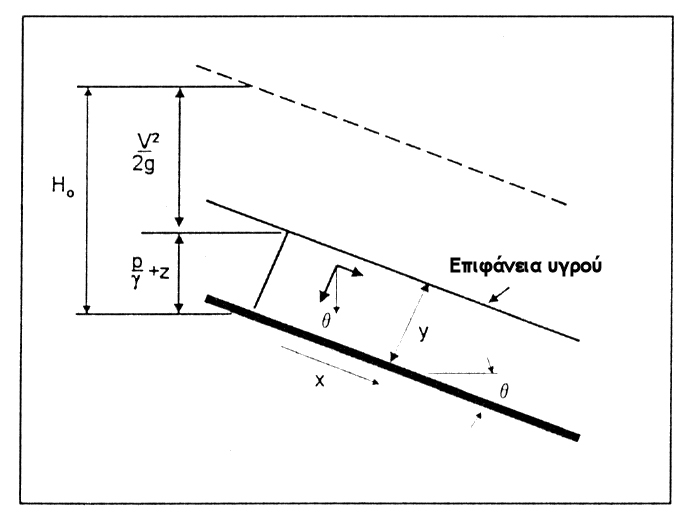
Σχήμα 3.3.5-2: Κατανομή πίεσης σε μόνιμη ομοιόμορφη ροή σε έντονες κλίσεις.