|
14.1. Γενικά
Η εξασφάλιση της αντοχής και της ευστάθειας των κατασκευών επιβάλλει την εξέταση της επιρροής των παραμορφώσεων στην εντατική κατάσταση (θεωρία 2ας τάξεως). Η φέρουσα ικανότητα ευλύγιστων κατασκευών ή ευλύγιστων μελών υπό θλίψη ενδέχεται να μειωθεί σημαντικά λόγω των φαινομένων 2ας τάξεως.
Η επιρροή των φαινομένων 2ας τάξεως θα αγνοείται εάν η σχετική αύξηση των καμπτικών ροπών 1ης τάξεως λόγω των παραμορφώσεων δεν είναι μεγαλύτερη του 10% (δηλαδή Ροπές 2ας τάξεως ≤ 10% Ροπών 1ης τάξεως).
Η εφαρμογή του Κεφαλαίου αυτού περιορίζεται σε μέλη από οπλισμένο και προεντεταμένο σκυρόδεμα υπό τη δράση αξονικού θλιπτικού φορτίου με ή χωρίς κάμψη, όπου οι επιρροές της στρέψης αγνοούνται.
14.2. Διαδικασία ελέγχου
Ο έλεγχος έναντι φαινομένων 2ας τάξεως πρέπει να εξασφαλίζει ότι, για τους πιο δυσμενείς συνδυασμούς των δράσεων στην οριακή κατάσταση αστοχίας, αφενός δεν θα υπάρξει υπέρβαση της αντοχής μεμονωμένων διατομών υπό τη δράση κάμψεως και αξονικής θλιπτικής δύναμης και αφετέρου δεν θα υπάρξει απώλεια ευστάθειας (τοπική ή στο σύνολο της κατασκευής).
Ο έλεγχος θα γίνεται προς κάθε διεύθυνση στην οποία ενδέχεται να υπάρξει αστοχία λόγω των φαινομένων 2ας τάξεως.
Ο ακριβής έλεγχος των φαινομένων 2ας τάξεως απαιτεί ανάλυση της κατασκευής με στατική 2ας τάξεως και εν συνεχεία αφενός έλεγχο έναντι μεγεθών ορθής εντάσεως των κρίσιμων διατομών των μελών και αφετέρου έλεγχο ευστάθειας των θλιβόμενων μελών της κατασκευής. Η ανάλυση αυτή είναι όμως δυσχερής λόγω της γεωμετρικής μη γραμμικότητας και της μη-γραμμικότητας των καταστατικών νόμων των υλικών (σκυροδέματος και χάλυβα). Για το λόγο αυτό επιτρέπεται ο έλεγχος μεμονωμένων υποστυλωμάτων και πλαισίων να γίνεται με προσεγγιστικές μεθόδους λεπτομέρειες των οποίων δίνονται στις επόμενες παραγράφους του Κεφαλαίου αυτού.
Η προσεγγιστική μεθοδολογία ελέγχου μεμονωμένων υποστυλωμάτων έναντι φαινομένων 2ας τάξεως συνοψίζεται στα εξής:
| • | Προσδιορισμός του εάν το υποστύλωμα είναι ευλύγιστο ή μη. Μόνο τα ευλύγιστα υποστυλώματα χρειάζεται να ελεγχθούν έναντι των φαινομένων 2ας τάξεως. |
| • | Επιλογή μεθοδολογίας ελέγχου των ευλύγιστων υποστυλωμάτων. |
| • | Για μεσαίες τιμές της λυγηρότητας επιτρέπεται η χρήση προσεγγιστικών μεθόδων ελέγχου, ενώ για μεγάλες τιμές της λυγηρότητας επιβάλλεται η χρήση ακριβών μεθόδων. |
Η προσεγγιστική μεθοδολογία ελέγχου πλαισίων έναντι φαινομένων 2ας τάξεως συνοψίζεται στα εξής:
| • | Προσδιορισμός του εάν το πλαίσιο είναι αμετάθετο ή μεταθετό. Ο σχεδιασμός κτιρίων με μεταθετά πλαίσια δέον να αποφεύγεται για λόγους αντισεισμικής συμπεριφοράς. |
| • | Τα αμετάθετα πλαίσια επιτρέπονται να αναλύονται με στατική 1ης τάξεως δηλαδή αγνοώντας τα φαινόμενα 2ας τάξεως στην ανάλυση, αλλά εν συνεχεία επιβάλλεται κάθε υποστύλωμα να ελέγχεται μεμονωμένα, με τα εντατικά μεγέθη που προέκυψαν από την ανάλυση, έναντι των φαινομένων 2ας τάξεως. |
14.3. Μεμονωμένα υποστυλώματα
14.3.1. Έλεγχος λυγηρότητας
Η λυγηρότητα λ ισούται με
![]() (14.1)
(14.1)
όπου:
l0 = ισοδύναμο μήκος το οποίο υπολογίζεται με βάση τη θεωρία ελαστικότητας.
i = ακτίνα αδράνειας του υποστυλώματος κατά την εξεταζόμενη διεύθυνση
![]() (14.2)
(14.2)
Ένα μεμονωμένο υποστύλωμα θεωρείται ευλύγιστο, εάν ικανοποιείται η ακόλουθη συνθήκη:
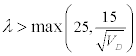 (14.3)
(14.3)
όπου:
VD ανηγμένη αξονική δύναμη σχεδιασμού
![]() (14.4)
(14.4)
Η μέγιστη επιτρεπόμενη λυγηρότητα είναι λMAX = 200.
14.3.2. Μέθοδοι υπολογισμού και απαλλαγές από τον έλεγχο.
α) Μέθοδοι υπολογισμού. Δίνονται τρία κριτήρια λυγηρότητας για την επιλογή της κατάλληλης μεθόδου υπολογισμού έναντι φαινομένων 2ας τάξεως:
| • | 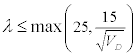 Το υποστύλωμα δεν θεωρείται ευλύγιστο και δεν απαιτείται έλεγχος έναντι φαινομένων 2ας τάξεως. Το υποστύλωμα δεν θεωρείται ευλύγιστο και δεν απαιτείται έλεγχος έναντι φαινομένων 2ας τάξεως. |
| • | 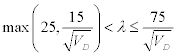 Το υποστύλωμα θεωρείται ευλύγιστο και ο έλεγχος έναντι φαινομένων 2ας τάξεως μπορεί να γίνει με απλοποιητικές μεθόδους, όπως η μέθοδος του προτύπου υποστυλώματος (παράγραφος 14.3.8) ή με άλλη απλοποιητική μέθοδο που δίνει συντηρητικά αποτελέσματα. Το υποστύλωμα θεωρείται ευλύγιστο και ο έλεγχος έναντι φαινομένων 2ας τάξεως μπορεί να γίνει με απλοποιητικές μεθόδους, όπως η μέθοδος του προτύπου υποστυλώματος (παράγραφος 14.3.8) ή με άλλη απλοποιητική μέθοδο που δίνει συντηρητικά αποτελέσματα. |
| • |
Κατά τον έλεγχο μεμονωμένων υποστυλωμάτων που ανήκουν σε αμετάθετα πλαίσια (παράγραφος 14.4.1) πρέπει επιπρόσθετα στα παραπάνω να ληφθεί υπόψη και το κριτήριο που δίνεται στην παράγραφο 14.4.3 για την περίπτωση ευλύγιστων υποστυλωμάτων.
β) Ερπυσμός
Η επιρροή του ερπυσμού μπορεί να παραλειφθεί εάν ικανοποιείται μία από τις παρακάτω συνθήκες:
e0/h ≥ 2.0 (14.5)
NG,K ≤ 0.2 NG+Q,K (14.6)
λ ≤ 70 (14.7)
όπου:
e0 εκκεντρότητα 1ης τάξεως = MSD/NSD
NG,K χαρακτηριστική τιμή της αξονικής δύναμης λόγω μακροχρόνιων δράσεων (οι οποίες προκαλούν ερπυσμό).
NG+Q,K χαρακτηριστική τιμή της αξονικής δύναμης λόγω του συνόλου των δράσεων.
14.3.3. Ισοδύναμο μήκος
Για κτίρια, το ισοδύναμο μήκος ενός υποστυλώματος ![]() μπορεί να προσδιοριστεί με βάση το Νομογράφημα του Σχήματος 14.1. που δίνεται παρακάτω, όπου οι συντελεστές KA και KB συμβολίζουν τις δυσκαμψίες πακτώσεως στα άκρα του υποστυλώματος.
μπορεί να προσδιοριστεί με βάση το Νομογράφημα του Σχήματος 14.1. που δίνεται παρακάτω, όπου οι συντελεστές KA και KB συμβολίζουν τις δυσκαμψίες πακτώσεως στα άκρα του υποστυλώματος.
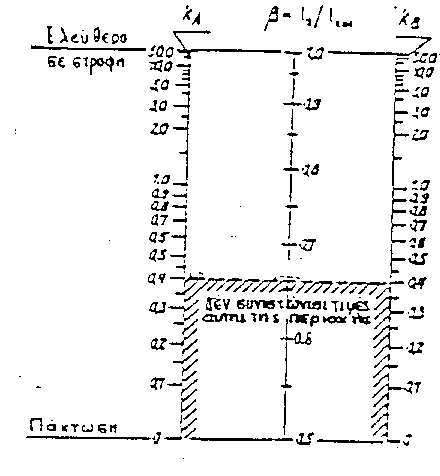
Σχήμα 14.1: Νομογράφημα για τον υπολογισμό του ισοδύναμου μήκους υποστυλωμάτων σε αμετάθετα πλαίσια.
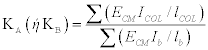 (14.8)
(14.8)
όπου:
ECM μέτρο ελαστικότητας του σκυροδέματος (παράγραφος 2.5.2)
ICOL, Ib ροπή αδράνειας (της πλήρους διατομής) του υποστυλώματος ή της δοκού αντιστοίχως
lCOL ύψος του υποστυλώματος μεταξύ των κέντρων των δεσμεύσεων στα άκρα
lb μήκος δοκού, μετρούμενο μεταξύ των κέντρων των πακτώσεων
n συντελεστής που λαμβάνει υπόψη τις συνθήκες πακτώσεως της δοκού στο απέναντί της άκρο.
| • | n = 1.0 για απέναντι άκρο ελαστικά ή πλήρως πακτωμένο. |
| • | η = 0.5 για απέναντι άκρο ελευθέρως στρεπτό. |
| • | η = 0 για δοκό πρόβολο. |
Τιμές του ΚA ή ΚB μικρότερες του 0.4 δεν συνιστώνται να χρησιμοποιούνται.
14.3.4. Πρόσθετη εκκεντρότητα
Για την κάλυψη ατελειών και αβεβαιοτήτων που δεν λαμβάνονται υπόψη στον υπολογισμό, πρέπει να λαμβάνεται υπόψη μια πρόσθετη εκκεντρότητα, ea του σημείου εφαρμογής της συνισταμένης των εξωτερικών αξονικών δυνάμεων, κατά την περισσότερο δυσμενή διεύθυνση, που δίνεται από τη σχέση:
eA = α Io/2 (14.9) όπου:
α απόκλιση του υποστυλώματος από την κατακόρυφο
![]() (14.10)
(14.10)
![]() όταν τα φαινόμενα 2ας τάξης δεν είναι αμελητέα
όταν τα φαινόμενα 2ας τάξης δεν είναι αμελητέα
hTOT είναι το ύψος του κτιρίου.
14.3.5. Εκκεντρότητες υπολογισμού
Η ολική εκκεντρότητα που πρέπει να λαμβάνεται υπόψη κατά τον υπολογισμό υποστυλώματος σταθερής διατομής (σκυροδέματος και οπλισμού, αγνοώντας τις παραθέσεις) στην πλέον εντεινόμενη διατομή (κρίσιμη διατομή) είναι:
eTOT = e0 + eA + e2 (14.11)
όπου:
e0 = εκκεντρότητα 1ης τάξεως = MSD1/NSD
MSD1 = δρώσα ροπή σχεδιασμού 1ης τάξεως
NSD = δρώσα αξονική δύναμη σχεδιασμού
eA = πρόσθετη εκκεντρότητα σύμφωνα με την εξίσωση (14.9)
e2 = εκκεντρότητα 2ας τάξεως, χρησιμοποιώντας τις προσεγγιστικές μεθόδους της παραγράφου 14.3.8, συμπεριλαμβάνοντας και την επιρροή του ερπυσμού.
Υπολογιστικό προσομοίωμα για τον υπολογισμό της εκκεντρότητας δίνεται στο Σχήμα 14.2, όπου οι εκκεντρότητες 1ης τάξεως e0,1 και e0,2 στα δύο άκρα λαμβάνονται υπόψη με τα πρόσημά τους.
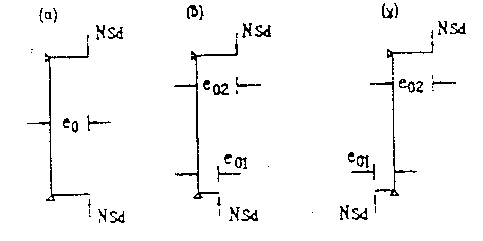
Σχήμα 14.2: Εκκεντρότητες στα άκρα υποστυλώματος.
α) ίσες e0 = e0,1 = e0,2
β) άνισες e0 = max ((0.6e0,2 + 0.4e0,1), 0.4e0,2)
γ) άνισες και ετερόσημες με (e0,2) ≥ (e0,1)
14.3.6. Επιρροή του ερπυσμού
Η επιρροή του ερπυσμού πρέπει εν γένει να λαμβάνεται υπόψη εάν οδηγεί σε σημαντική αύξηση των φαινομένων 2ας τάξεως. Δεν απαιτείται να ληφθεί υπόψη όταν ισχύουν οι συνθήκες της παραγράφου 14.3.2)β.
Για την αντιμετώπιση της επιρροής του ερπυσμού επιτρέπεται η χρήση προσεγγιστικών μεθόδων.
Οι ερπυστικές παραμορφώσεις που λαμβάνονται υπόψη, προκαλούνται από τις μακροχρόνιες δράσεις αυξημένες με τον επιμέρους συντελεστή ασφαλείας του ερπυσμού, ο οποίος λαμβάνεται ίσος με 1,20.
14.3.7. Ακριβής μέθοδος υπολογισμού
Ο υπολογισμός των εντατικών μεγεθών γίνεται με την θεωρία 2ας τάξεως και σύμφωνα με τις παρακάτω γενικές αρχές:
α) Τα διαγράμματα τάσεων - παραμορφώσεων του σκυροδέματος και του οπλισμού λαμβάνονται σύμφωνα με τις παραγράφους 10.4.3.1 και 10.4.4 και το μέτρο ελαστικότητας από τον Πίνακα 2.2. Δεν επιτρέπεται εν γένει να λαμβάνεται υπόψη η συνεργασία του σκυροδέματος σε εφελκυσμό στην ρηγματωμένη διατομή.
β) Εκτός από τις εκκεντρότητες πρώτης τάξεως λαμβάνονται υπόψη στον υπολογισμό οι πρόσθετες εκκεντρότητες λόγω γεωμετρικών ατελειών (παράγραφος 14.3.4) και ερπυσμού (παράγραφος 14.3.6). Εκκεντρότητες λόγω θερμοκρασιακών επιρροών και συστολής ξήρανσης δεν λαμβάνονται γενικώς υπόψη.
14.3.8. Μέθοδος προτύπου υποστυλώματος
Όρια ισχύος
Η μέθοδος αυτή εφαρμόζεται μόνον όταν λ ≤ 140 ή ![]() και σε ορθογωνικές ή κυκλικές διατομές στις οποίες η εκκεντρότητα 1ης τάξεως ικανοποιεί τη συνθήκη e0 ≥ 0.1 h (h = ύψος της διατομής στο επίπεδο υπό έλεγχο).
και σε ορθογωνικές ή κυκλικές διατομές στις οποίες η εκκεντρότητα 1ης τάξεως ικανοποιεί τη συνθήκη e0 ≥ 0.1 h (h = ύψος της διατομής στο επίπεδο υπό έλεγχο).
Ορισμός
Πρότυπο υποστύλωμα είναι ένας στύλος που:
| • | είναι πακτωμένος στη βάση και ελεύθερος στην κορυφή, |
| • | κάμπτεται με απλή καμπυλότητα λόγω φορτίων (αξονικών ή συγκεντρωμένων / κατανεμημένα οριζόντιων) ή / και ροπής στην κορυφή, |
| • | έχει πρακτικώς σταθερές διαστάσεις διατομής και οπλισμούς καθ ύψος |
| • | το μέγιστο βέλος e2 (εκκεντρότητα 2ας τάξεως) και η καμπυλότητα, 1/r στη βάση του υποστυλώματος μπορούν να θεωρηθούν ότι συνδέονται μέσω της προσεγγιστικής σχέσης: |
![]() (14.12) όπου:
(14.12) όπου:
I0 = ισοδύναμο μήκος = 2 l
K1 = λ/20 - 0.75 για 15 ≤ λ ≤ 35
K1 = 1 για 35 < λ.
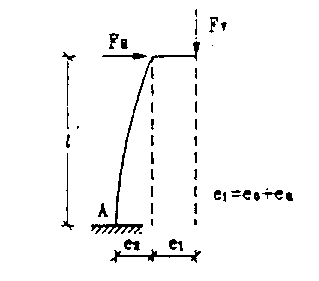
Σχήμα 14.3: Πρότυπο υποστύλωμα.
Εφαρμογές της μεθόδου
Ξεκινώντας από τα διαγράμματα ροπών αντοχής MRD καμπυλοτήτων 1/r στην κρίσιμη διατομή, για διάφορες τιμές της δρώσας αξονικής δύναμης NSD είναι δυνατόν να δοθεί σε μορφή πινάκων η διαθέσιμη ροπή αντοχής μετά την αφαίρεση των επιρροών 2ας τάξεως.
Σε περιπτώσεις όπου δεν χρειάζεται μεγάλη ακρίβεια, η καμπυλότητα 1/r στην εξίσωση (14.12) μπορεί να υπολογιστεί απλοποιητικά από τη σχέση
![]() (14.13)
(14.13)
όπου:
εYD παραμόρφωση σχεδιασμού στο όριο διαρροής του οπλισμού = fYD/ES
d στατικό ύψος της διατομής κατά την ελεγχόμενη διεύθυνση
![]() (14.14)
(14.14)
όπου:
NRD αξονικό φορτίο αντοχής σχεδιασμού = 0.85 fCD AC + fYD AS
NSD δρον αξονικό φορτίο σχεδιασμού
NBAL φορτίο, το οποίο όταν ασκείται στη διατομή μεγιστοποιείται η ροπή αντοχής. Για συμμετρικά οπλισμένες διατομές μπορεί να ληφθεί προσεγγιστικά ίσο με 0.4 fCD AC
Θα είναι πάντα συντηρητική η παραδοχή του K2 = 1.
14.3.9. Διαξονική Κάμψη
Ο έλεγχος υποστυλωμάτων υπό διαξονική κάμψη με αξονική θλιπτική δύναμη έναντι φαινομένων 2ας τάξεως, πρέπει εν γένει να γίνει με κατάλληλες ακριβείς μεθόδους.
Σε υποστυλώματα ορθογωνικής διατομής επιτρέπονται χάριν απλοποιήσεως να γίνουν χωριστοί έλεγχοι έναντι φαινομένων 2ας τάξεως στα δύο κύρια επίπεδα y και z (δηλαδή δύο έλεγχοι μονοαξονικής κάμψεως και θλιπτικής δύναμης) υπό την προϋπόθεση ότι οι λόγοι των αντιστοίχων εκκεντρότητων eY/b και eZ/h ικανοποιούν μία από τις παρακάτω συνθήκες:
(eZ/h) / (eY/b) ≤ 0.2 (14.15)
(eY/b) / (eZ/h) ≤ 0.2 (14.16)
Οι εκκεντρότητες eY και eZ είναι οι εκκεντρότητες 1ης τάξεως στην κατεύθυνση των διαστάσεων b και h της διατομής αντιστοίχως. Οι γεωμετρικές ατέλειες της παραγράφου 14.3.4 θα πρέπει να λαμβάνονται υπόψη στα επίπεδα των δύο χωριστών ελέγχων.
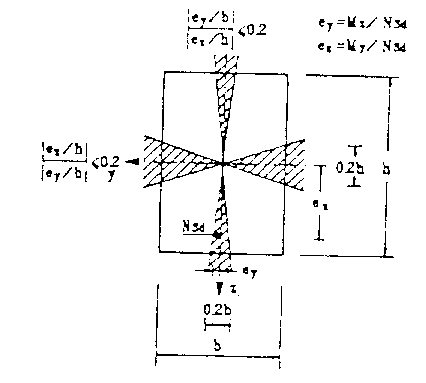
Σχήμα 14.4: Παραδοχή για χωριστούς ελέγχους στα δυο κύρια επίπεδα.
Εάν eZ > 0.2 h στους παραπάνω χωριστούς ελέγχους, πρέπει ο έλεγχος για κάμψη περί τον δευτερεύοντα άξονα της διατομής (z στο παρακάτω σχήμα) να βασίζεται στο μειωμένο πλάτος h' όπως δίνεται στο σχήμα 14.5. Η τιμή του h' μπορεί να προσδιοριστεί με την παραδοχή της γραμμικής κατανομής των τάσεων, δηλαδή από τη σχέση:
NSD/AC - NSD (eZ + eAZ)/WC = 0 (14.17)
όπου:
WC ροπή αντιστάσεως
eAZ πρόσθετη εκκεντρότητα λόγω γεωμετρικών ατελειών (παράγραφος 14.3.4) στη διεύθυνση z.
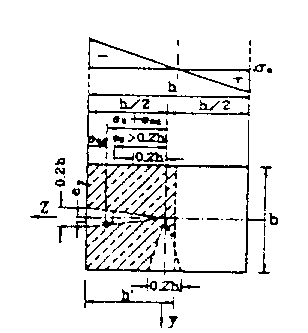
Σχήμα 14.5: Χωριστός έλεγχος περί τον δευτερεύοντα άξονα όταν eZ > 0.2 h.
Εάν δεν ικανοποιείται μία από τις συνθήκες (14.15) ή (14.16) τότε απαιτείται ακριβής ανάλυση.
14.4. Πλαίσια
Υπάρχουν δύο κατηγορίες πλαισίων: τα μεταθετά και τα αμετάθετα. Αμετάθετα είναι τα πλαίσια των οποίων οι κόμβοι παρουσιάζουν μηδενικές ή πολύ μικρές μετατοπίσεις υπό τις δράσεις σχεδιασμού, σε αντίθεση με τα μεταθετά των οποίων οι κόμβοι παρουσιάζουν σημαντικές οριζόντιες μετατοπίσεις.
Πιο συγκεκριμένα αμετάθετα είναι τα πλαίσια στα οποία η σχετική αύξηση των καμπτικών ροπών λόγω των παραμορφώσεων δεν είναι μεγαλύτερη από 10% (δηλαδή ροπές 2ας τάξεως ≤ 10% ροπών 1ης τάξεως). Θεωρείται ότι ο έλεγχος αυτός εξασφαλίζεται μέσω των πρακτικών κριτηρίων αμεταθετότητας που δίνονται στην παράγραφο 14.4.1.
Για λόγους αντισεισμικής συμπεριφοράς δεν συνίσταται εν γένει ο σχεδιασμός μεταθετών πλαισίων.
14.4.1. Ορισμός αμεταθετότητας πλαισίων
Τα πλαίσια μπορούν να θεωρηθούν ως αμετάθετα όταν ικανοποιούνται οι προϋποθέσεις της παραγράφου α που ακολουθεί:
α) Εάν σε κάθε όροφο ικανοποιείται η σχέση:
![]() (14.18)
(14.18)
όπου:
θ συντελεστής ευστάθειας
FDV συνολικό κατακόρυφο φορτίο πάνω από τον εξεταζόμενο όροφο στην οριακή κατάσταση αστοχίας.
δ διαφορά βελών στον υπόψη όροφο λόγω των οριζοντίων φορτίων (σχετικό βέλος ορόφου). Εάν οι παραμορφώσεις δ υπολογισθούν με ακαμψίες σταδίου Ι το όριο στην εξίσωση (14.18) πρέπει να λαμβάνεται ίσο με 0.06 (αντί 0.10)
FDH συνολική οριζόντια δύναμη που ενεργεί πάνω από τον υπόψη όροφο στην οριακή κατάσταση αστοχίας.
h ύψος ορόφου
Για οριζόντια φορτία λόγω σεισμικών δράσεων το σχετικό βέλος ορόφων δ ισούται με αυτό που υπολογίζεται από την ανάλυση για τα φορτία του κατάλληλου συνδυασμού της παραγράφου 6.4.1 πολλαπλασιασμένο με τον δείκτη συμπεριφοράς.
β) Το κριτήριο της παραπάνω παραγράφου α ικανοποιείται συνήθως εάν τα κατακόρυφα στοιχεία ακαμψίας είναι επαρκώς συμμετρικά κατανεμημένα μέσα στο κτίριο και ικανοποιείται μία από τις ακόλουθες σχέσεις:
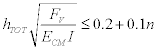 για n ≤ 3 (14.19)
για n ≤ 3 (14.19)
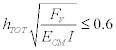 για n ≥ 4 (14.20)
για n ≥ 4 (14.20)
όπου:
n = αριθμός ορόφων
hTOT ολικό ύψος κατασκευής μετρούμενο από την υποτιθέμενη πάκτωση (δηλαδή στάθμη εδάφους ή στάθμη οροφής πρακτικά απαραμόρφωτων υπογείων)
ECMI συνολική ακαμψία σταδίου I των κατακόρυφων στοιχείων (π.χ. τοιχώματα ή υποστυλώματα μη διακοπτόμενα καθ ύψος) που εξασφαλίζουν το αμετάθετο των κόμβων κατά την υπόψη διεύθυνση (βλέπε παράγραφο 2.5.2. για το ECM). Τα κατακόρυφα αυτά στοιχεία πρέπει να έχουν σταθερή διατομή σε όλο το ύψος του κτιρίου, διαφορετικά θα υπολογίζεται μια ισοδύναμη ακαμψία. Η ακαμψία των υποστυλωμάτων λαμβάνεται υπόψη εάν στη δεδομένη διεύθυνση σε όλους τους ορόφους συντρέχουν σε κόμβους με δοκούς ώστε να είναι δυνατός ο σχηματισμός πλαισίου.
FV άθροισμα όλων των κατακόρυφων φορτίων λειτουργίας (GΚ + QΚ).
14.4.2. Πρόσθετη κλίση
Για κάλυψη διαφόρων επιρροών που λαμβάνονται προσεγγιστικά υπόψη στον υπολογισμό πρέπει να λαμβάνεται υπόψη μια πρόσθετη κλίση α όλων των κατακόρυφων στοιχείων (υποστυλώματα, τοιχεία κ.λ.π.) ως προς την κατακόρυφο με τιμή:
![]() (14.21)
(14.21)
όταν τα φαινόμενα 2ας τάξης είναι αμελητέα
![]()
όταν τα φαινόμενα 2ας τάξης δεν είναι αμελητέα
Επιπρόσθετα επιτρέπεται για την περίπτωση κτιρίων με υποστυλώματα, που σε όλους τους ορόφους συντρέχουν σε κόμβους με δοκούς, ώστε να είναι δυνατός ο σχηματισμός πλαισίου στη δεδομένη διεύθυνση, να πολλαπλασιάζεται η παραπάνω τιμή του α επί τον μειωτικό συντελεστή:
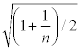
όπου:
η ο αριθμός των στηλών υποστυλωμάτων
14.4.3. Υπολογισμός αμετάθετων πλαισίων
Ο ακριβής έλεγχος των φαινομένων 2ας τάξεως σε κτίρια απαιτεί ανάλυση του πλαισίου με στατική 2ας τάξεως, και εν συνεχεία αφενός έλεγχο έναντι μεγεθών ορθής εντάσεως των κρίσιμων διατομών των μελών και αφετέρου έλεγχο ευστάθειας των θλιβόμενων μελών της κατασκευής. Επιτρέπεται όμως ο υπολογισμός αμετάθετων πλαισίων να γίνει απλοποιητικά σε δύο στάδια:
α) Κατ' αρχήν γίνεται ανάλυση του πλαισίου με τη θεωρία της 1ης τάξεως λαμβάνοντας υπόψη τις πρόσθετες κλίσεις της παραγράφου 14.4.2 και
β) Κατόπιν γίνεται έλεγχος κάθε υποστυλώματος έναντι φαινομένων 2ας τάξεως, θεωρώντας κάθε υποστύλωμα ως μεμονωμένο, σύμφωνα με την παράγραφο 14.3. Στους ελέγχους αυτούς όσα μεμονωμένα υποστυλώματα έχουν λυγηρότητα μικρότερη ή ίση από την τιμή που δίνεται στην εξίσωση (14.22), και δεν φέρουν εγκάρσια φορτία μεταξύ των άκρων τους, δεν χρειάζεται να ελεγχθούν για φαινόμενα 2ας τάξεως ακόμη και εάν το υποστύλωμα είναι ευλύγιστο κατά τις παραγράφους 14.3.1 και 14.3.2.
λCRIT = 25 (2 - e0,1 / e0,2 (14.22) όπου:
οι εκκεντρότητες e0,1 και e0,2 του αξονικού φορτίου στα δύο άκρα του μέλους ορίζονται στο Σχήμα 14.2 (με αλγεβρικά πρόσημα και | e0,2 | ≥ | e0,1 |).
Στην περίπτωση αυτή, τα άκρα του υποστυλώματος θα πρέπει να σχεδιαστούν για τουλάχιστον τις συνθήκες που δίνονται από τις εξισώσεις (14.23) και (14.24).
NRD = NSD (14.23)
MRD = NSD h/20 (14.24)
όπου:
NRD τιμή σχεδιασμού της αξονικής δύναμης αντοχής σε θλίψη.
MRD τιμή σχεδιασμού της ροπής αντοχής.


