|
8.1. Μέθοδοι ανάλυσης
Η επίλυση του δομικού συστήματος γίνεται με την θεωρία της ελαστικότητας που μπορεί να είναι γραμμική (παράγραφος 8.2.1) η γραμμική με περιορισμένη ανακατανομή (παράγραφος 8.2.2) καθώς και με τη θεωρία της πλαστικότητας (παράγραφος 8.3).
Η μέθοδος ανάλυσης πρέπει να βασίζεται σε ένα αξιόπιστο αναλυτικό ομοίωμα της κατασκευής.
8.2. Ελαστική ανάλυση
Η μέθοδος αυτή βασίζεται στη θεωρία ελαστικότητας. Οι μετατοπίσεις μπορεί να είναι μικρές (θεωρία 1ης τάξης) ή μεγάλες (θεωρία 2ης τάξεως).
8.2.1. Γραμμική ελαστική ανάλυση
Η γραμμική ελαστική ανάλυση εφαρμόζεται για ελέγχους οριακών καταστάσεων αστοχίας και οριακών καταστάσεων λειτουργικότητας.
Ο προσδιορισμός των δυσκαμψιών για την επίλυση στατικώς αορίστων συστημάτων γίνεται γενικώς στο στάδιο Ι με βάση τις ονομαστικές ή ιδεατές διατομές (παράγραφος 7.2.3).
8.2.2. Γραμμική ελαστική ανάλυση με περιορισμένη ανακατανομή
8.2.2.1. Γενικά
Για τον έλεγχο οριακών καταστάσεων αστοχίας επιτρέπεται ανακατανομή των ροπών που προέκυψαν από την γραμμική ανάλυση.
Οι συνέπειες της ανακατανομής των ροπών πρέπει να λαμβάνονται υπόψη για όλα τα εντατικά μεγέθη (π.χ. και για τις τέμνουσες), ώστε να ικανοποιούνται οι εξισώσεις ισορροπίας.
Η δυνατότητα ανακατανομής εξαρτάται από την πλαστιμότητα της διατομής, η οποία είναι συνάρτηση του λόγου x/d όπου x το ύψος της θλιβόμενης ζώνης της υπόψη διατομής και d το στατικό της ύψος.
8.2.2.2. Συνθήκες πλαστιμότητας
Επιτρέπεται η μείωση των μεγίστων ροπών κάμψεως με τον πολλαπλασιασμό επί τον συντελεστή δ ο οποίος προσδιορίζεται από την εξίσωση:
0.5 + 1.25 x/d < δ < 1,0 (8.1)
όταν ικανοποιούνται οι παρακάτω συνθήκες:
α) για συνεχείς δοκούς και αμετάθετα πλαίσια δ > 0.70 (8.2)
β) x/d ≤ 0.45 για σκυρόδεμα C12 έως C35 (8.3A)
x/d ≤ 0.35 για σκυρόδεμα C40 και άνω (8.3B)
8.3. Πλαστική ανάλυση
Η πλαστική ανάλυση επιτρέπεται να εφαρμόζεται μόνον για τον έλεγχο οριακών καταστάσεων αστοχίας υφισταμένων κατασκευών.
Η πλαστική ανάλυση γίνεται με βάση τη θεωρία πλαστικών αρθρώσεων, όπου οι πλαστικές παραμορφώσεις (πλαστικές στροφές), θεωρούνται συγκεντρωμένες σε ορισμένες διατομές του φορέα. Η επιτρεπόμενη τοπική πλαστική στροφή για χάλυβες με ικανοποιητική ολκιμότητα μπορεί να ληφθεί από το παρακάτω διάγραμμα, το οποίο δεν λαμβάνει υπόψη την ευμενή επιρροή του εγκάρσιου οπλισμού και ισχύει για διπλές πλαστικές αρθρώσεις στο μέσο δοκών με l:h ίσο ή κατά προσέγγιση ίσο με 6.
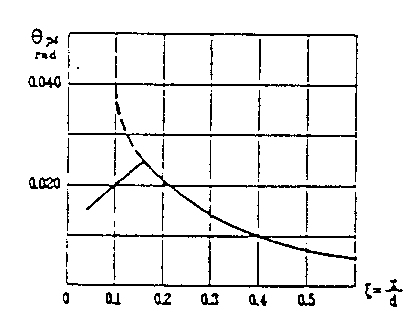
Σχήμα 8.1: Επιτρεπόμενη πλαστική στροφή
Η ανάλυση είναι δυνατόν να γίνει και με ελαστοπλαστικές μεθόδους. Σε αυτή την περίπτωση για τα διαγράμματα ροπών-καμπυλοτήτων είναι συχνά ικανοποιητική η υιοθέτηση διγραμμικών παραστάσεων που περιγράφουν:
| • | το στάδιο I: σκυρόδεμα μη ρηγματωμένο, γραμμική-ελαστική συμπεριφορά. |
| • | το στάδιο II: σκυρόδεμα ρηγματωμένο. |
Για τα διαγράμματα ροπών-στροφών μπορεί να υιοθετηθεί μια τριγραμμική παράσταση που περιγράφει και το στάδιο III, της ανάπτυξης πλαστικής στροφής ΘPL στη διατομή.
8.4. Συνεργαζόμενο πλάτος πλακοδοκών
Σε περιπτώσεις διατομών όπου η επιρροή της διάτμησης είναι σημαντική δεν ισχύει ο νόμος της επιπεδότητας των διατομών. Για την απλοποίηση των υπολογισμών εισάγεται το συνεργαζόμενο πλάτος των διατομών και ο νόμος της επιπεδότητας θεωρείται ότι εξακολουθεί να ισχύει. Οι τιμές του συνεργαζόμενου πλάτους μπορούν να χρησιμοποιηθούν για τις οριακές καταστάσεις αστοχίας και λειτουργικότητας.
8.5. Δυστρεψία
Σε περίπτωση έλλειψης ακριβέστερων στοιχείων για τον υπολογισμό εντατικών μεγεθών θα χρησιμοποιούνται οι παρακάτω τιμές, οι οποίες μπορούν να ληφθούν σταθερές για όλο το μήκος κάθε ανοίγματος.
KL = 0.30 ECC / (1 + 1,0 φ) (8.4)
KLLM = 0.10 ECC / (1 + 0,3 φ) (8.5)
KLLT = 0.05 ECC / (1 + 0,3 φ) (8.6)
όπου:
KL = δυστρεψία σταδίου I, απουσία ρωγμών.
KLLM = δυστρεψία σταδίου II, καμπτικές ρωγμές.
KLLT = δυστρεψία σταδίου II, ρωγμές λόγω στρέψης και τέμνουσας.
C = στρεπτική ροπή αδράνειας στην μη ρηγματωμένη κατάσταση.
φ = συντελεστής ερπυσμού από τον Πίνακα 2.4 για φορτίσεις μακράς διαρκείας.


